Find an answer to your question "What are the domain and range of the function f (x) = 3X 5?O domain (00,00);Find the Domain and Range f (x)=5 f (x) = −5 f ( x) = 5 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x Explanation The denominator of f (x) cannot be zero as this would make f (x) undefined Equating the denominator to zero and solving gives the value that x cannot be solve x = 9 = 0 ⇒ x = 9 ← excluded value ⇒ domain is x ∈ R,x ≠ 9 for the range rearrange making x the subject y = 5 x −9

View Question What Are The Domain And Range Of The Function
F(x)=2x+5 domain and range
F(x)=2x+5 domain and range-In f(x) = 5(x3)²= x²6x4 , x has no impediment in the Real scale so the domain must be all Real x In the range we see that for f(x)=0 there are the real roots x=(6±√)/2 and just as with the domain no reason to except any Real numbers in the range either, now we check for maxima and/or minnima f'(x)=2x6 and when x=3 and f(x)=5 there's a maximum so the domain in the positive Identify the vertex, axis of symmetry, minimum or maximum, domain, and range of the function f(x) = (x 4)2 – 5 Categories Uncategorized Leave a Reply Cancel reply Your email address will not be published Required fields are marked * Comment Name * Email *




Find Domain And Range Of Function Y 1 X Youtube
For this function any whole number is okay,then use PEMDAS to compute the range Good rule of thumbs on domain and range constants have any number as the domain f(X)= 7, then (1,7),(2,7),(3,7) Linear functions in the slope intercept method neGiven f(x) = x 5 ∀ x є R To Find Domain and Range of f(x) The domain of the given function is all real numbers expect where the expression is undefined In this case, there is no real number which makes the expression undefined As f(x) is a polynomial function, we can have any value of x Therefore, Domain(f) = (∞, ∞) {x x є RTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)`
To find the range we have to study the behavior for x → ± ∞ lim x→−∞ f (x) = lim x→ −∞ 5 x − 9 = 5 −∞ = 0− lim x→∞ f (x) = lim x→ ∞ 5 x − 9 = 5 ∞ = 0 Then y = 0 is a horizontal asymptote Indeed, f (x) ≠ 0∀x ∈ FE x → 9±One way to include negatives is to reflect it across the x axis by adding a negative y = x^2 With this y cannot be positive and the range is y≤0 The other way to include negatives is to shift the function down So y = x^2 2 shifts the whole function down 2 units, and y ≥ 2 Transcript Example 21 Find the domain of the function "f" (x) = (" " 2 3 5)/( 2 5 4) "f" (x) = (" " x2 3x 5)/(x2 5x 4) = (x2 3x 5)/(x2 4x 4) = (x2 3x 5)/( (x 4) 1( 4)) = (x2 3x 5)/(( 4)(x 1) ) In real numbers , the denominator cannot be zero Hence (x 4) (x 1) 0 x 4 and x 1 Hence the domain of the function will be all real numbers except 1 and 4 Hence, the domain
Domain and range The domain and range of a function is all the possible values of the independent variable, x, for which y is defined The range of a function is all the possible values of the dependent variable y The example below shows two different ways that a function can be represented as a function table, and as a set of coordinatesArrow_forward Question View transcribed image text fullscreen Expand check_circle Expert Answer Want to see the stepbystep answer?Answer to Find the maximal domain and range of the function f, given by f(x) = \sqrt{5 4x x^2}, and sketch its graph By signing up, you'll get




Section 1 1 Relations And Functions Relation Domain Range Function Example 1 State The Domain And Range Of Each Relation Then State Whether Ppt Download




Domain Range A Find The Natural Domain 3 1 F X Chegg Com
Range (0,0) O domain (3,0);Find the Domain and Range f (x)=x5 f (x) = x − 5 f ( x) = x 5 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xAir TutorsQuestion Graph and find the domain and range of h(x) = 3x^2 5
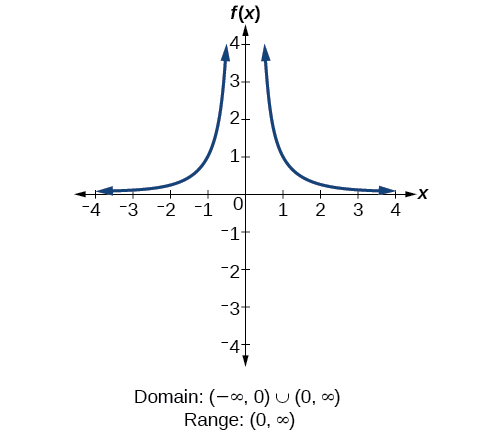



Domain And Range Algebra And Trigonometry




Calculate G X Where G F 1 State The Domain And Chegg Com
For the square root function latexf\left(x\right)=\sqrt{x}/latex, we cannot take the square root of a negative real number, so the domain must be 0 or greater The range also excludes negative numbers because the square root of a positive number latexx/latex is defined to be positive, even though the square of the negative number latex\sqrt{x}/latex also gives us latexx/latexIf f(x) = 3x 4, find f(5) and f(x 1) f(5) = 3(5) 4 = 19 f(x 1) = 3(x 1) 4 = 3x 7 Domain and Range The domain of a function is the set of values which you are allowed to put into the function (so all of the values that x can take) The range of theWhat is domain and range?




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
Popular Problems Algebra Find the Domain and Range f (x) = log of x5 f (x) = log(x − 5) f ( x) = log ( x 5) Set the argument in log(x−5) log ( x 5) greater than 0 0 to find where the expression is defined x−5 > 0 x 5 > 0 Add 5 5 to both sides of the inequality x > 5 x > 5 The domain is all values of x x that make the expression definedVerified by Toppr f (x) = x−5 For f (x) to be defined, the term under the Squareroot should be greater than or equal to zero x−5 ≥ 0 x ≥ 5 So, the domain is 5,∞) Now, for x−5≥ 0 x−5Let F (x) = y = (x 5)/ (x 3) Clearly F (x) or y is well defined for all real x, except x = 3 Therefore domain of F ie D (F) = R {3} Next, for the range of F (x), we have;




Example 21 Find Domain Of F X X2 3x 5 X2 5x 4
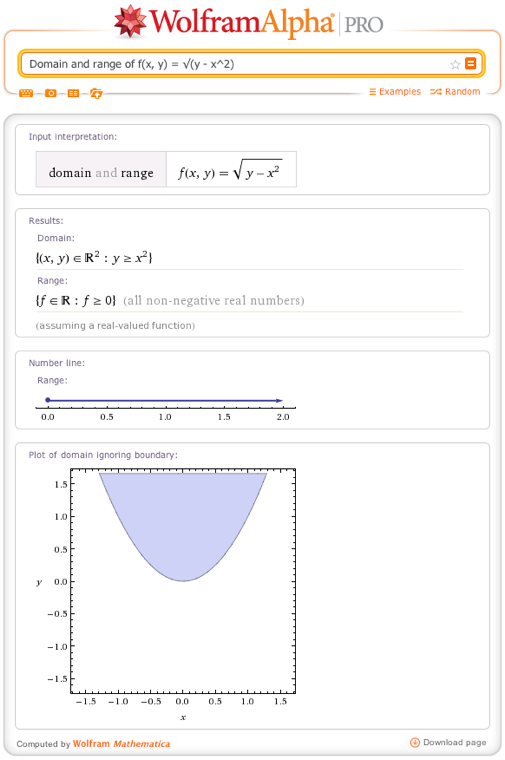



Solve Domain And Range Of A Function With Wolfram Alpha Wolfram Alpha Blog
How to recognize the domain and range of a function by considering the possible inputs and outputs of a functionWe can also graph a function to find its domDoman = R,Range =(−∞,2 Given f (x)= 2−∣x−5∣ Domain of f (x) is defined for all real values of x Since, ∣x−5∣ ≥0 −∣x−5∣ ≤0 2−∣x−5∣ ≤2 f (x) ≤2 Hence, range of f (x) is (−∞,2The domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2




4 Ways To Find The Range Of A Function Wikihow
Correct answers 2 question What are the domain and range of the function f(x) = 3x 5?If you meant f (x) = 15/x 5, the point excluded from the domain is 0, and the point excluded from the range is 5 It's the function above translated to th Continue Reading This is similar to the familiar hyperbola f (x) = 1/x For f (x) = 15 / (x 5), the domain does not include x = 5The domain of the realvalued function f (x) = lo g 1 0 (x 1) (x − 4) (3 − x) (x 2) does not contain the intervals (− ∞, − 5) and (5, 6) Hard View solution



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora
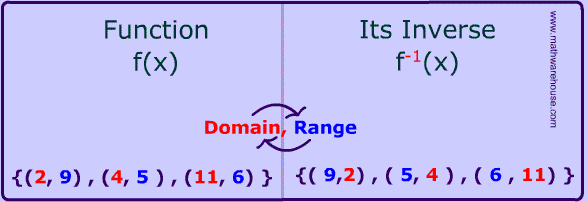



Inverse Of A Function In Math Tutorial Explaining Inverses Step By Step Several Practice Problems Plus A Free Worksheet With Answer Key
First week only $499!Verified by Toppr f(x)= x−5 For f(x) to be defined, the term under the Squareroot should be greater than or equal to zero x−5≥0 x≥5 So, the domain is 5,∞) Now, for x−5≥0 x−5See Answer Check out a sample Q&A here




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic



Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf
Given f (x) = 1/√x−5 To find the domain and range of function Explanation So, the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞) Domain and range of f (x)=5 The absolute value of x 5 is equal to x 5 for x 5 0 and it is equal to x 5 for x 5 0 How to recognize the domain and range of a function by considering the possible inputs and outputs of a functionWe can also graph a function to find its dom Xx R x x ℝ As for the range weFind the Domain and Range f (x)=5/x f (x) = 5 x f ( x) = 5 x Set the denominator in 5 x 5 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval Notation




1 Identify Relations Domains And Ranges 2 Identify Functions



Domain And Range Of A Function
Find the Domain and Range f(x)=x The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation SetBuilder Notation The absolute value expression has a V shape All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ( (9 −x^2)) It is given that the function is a real functionSolution For The domain and range of y =f(x)= \cos (\log x) are Solution For The domain and range of y =f(x)= \cos (\log x) are Become a Tutor Blog Cbse Question Bank Pdfs Micro Class Download App Class 11 Math All topics Relations and Functions II 508 150 The domain




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Find The Domain And Range Of The Following Real Functions I F X X Ii F X Sqrt 9 X 2 Youtube
Range (5,00) domain " in 📘 Mathematics if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questionsRange set includes those values of f(x)(called functional values) for which x is in the domain That is all the numbers that can be generated from this function f(x)=(x3)/(2x1) for each x in the domain Example , put x=1 then f(1)=(2/3) So (2/3) is a member of the range set Now here is how to chose the range elements Set y=(x3)/(2x1)Range The out comes or values that we get for y is known as range Domain for given function f (x) = x 3 For any real values of x, f (x) will give defined values Hence the domain is R Since we have absolute sign, we must get only positive values by applying any positive and negative values for x in the given function




L1 Functions Domain Amp Range



The Domain And Range Of The Function F Given By F X 2 X 5 Is Youtube
Given that f(x) = 1/√(x 5) Here, it is clear that (x) is real when x – 5 > 0 ⇒ x > 5 Hence, the domain = (5, ∞) Now to find the range put For x ∈ (5, ∞), y ∈ R Hence, the range of fRange (5,0) O domain (0coFind the domain and range of the function `f(x)=(1)/sqrt(x5)`




Find The Domain And Range Of The Function F X 1 Sqrt X 5 Youtube




View Question What Are The Domain And Range Of The Function
Range (000) domain (00,00);Determine the domain and range for the relation = {(x, y)\x is the sister of y} close Start your trial now! First we can conisder the domain, this is fairly simple, we must consider what values of x yields a valid value of f (x), and we see for all values of x, f (x) is defined, and we can see that by a sketch;




Determine The Domain And Range Of The Function F X Chegg Com




Find The Domain Of The Range Of Each Of The Following Real Functions F X Sqrt 3x 5 Youtube
f (x) = log (x) 5 We note that the function is defined for all positive x values because log (0) is NOT defined The range of the function is all real numbers because the function f (x) can take positive and negative values Answer option 1 domain x> 0The domain of a function, D D, is most commonly defined as the set of values for which a function is defined For example, a function f (x) f ( x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function isDoman= R,Range= (−∞,2 Given f (x)= 2−∣x−5∣ Domain of f (x) is defined for all real values of x Since, ∣x−5∣ ≥0 −∣x−5∣ ≤0 2−∣x−5∣ ≤2 f (x) ≤2 Hence, range of f (x) is (−∞,2
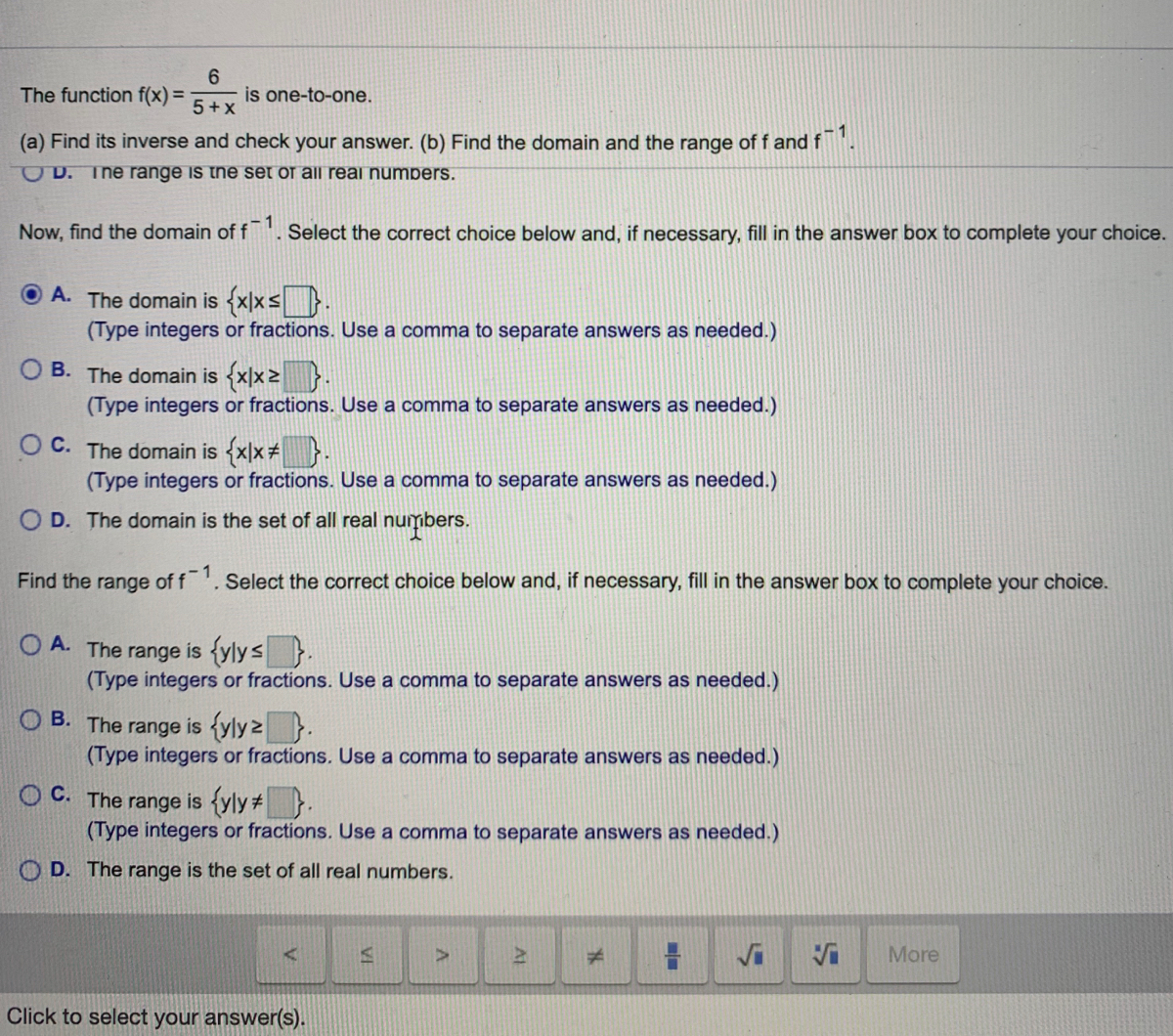



Answered 6 The Function F X Is One To One Bartleby



Domain Range Power
The range of fg is given by f(g(x)) ≥ −8 So in this case, the range of the composed function f(g(x)) is contained in the range of f, but it is not the whole of the range of f And in general, the range of a composed function is either the same as the range of the second function, or else lies inside itCreate your account View this answer We are given the quadratic function f(x) = x2−5 f ( x) = x 2 − 5 Solving for its domain and range, we haveY = (x5)/ (x3) ==>x = (3y 5)/ (1y) which exist every where except y = 1 Therefore, range of F = R { 1 }




Section 1 5 Combinations Of Functions Ppt Download




Find The Domain And Range Of F X 2 5x 3x 4
Graph {2x^28x5 858, 1142, 436, 564} To consider the range, we must cosnider all the values f (x) can take on, and by the sketch, we see the the max value of f (x) is 3, Domain (∞,∞) Range (5,∞) Option 2 is correct Stepbystep explanation Given It is an exponential function with base 3 Domain It is input value of x for which function defined All real number Range It is output value of y for all defined value of x (c,∞) For given functionDomain and Range Domain The domain of the function is defined by the values of the function on the xaxis Range The range of the function is defined by the values of the function on the yaxis




How To Find The Domain And Range Of A Function 14 Steps




What Is Domain And Range In A Function Video Lesson Transcript Study Com




Functions Domain Range Exclusions Edexcel Igcse Maths Revision Notes




10 Find The Domain And Range A F X V X 2 5 X
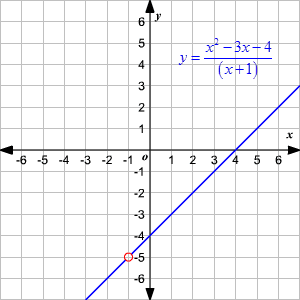



Domain And Range Of Rational Functions




Ex 2 3 5 Find The Range Of Function F X 2 3x X R X 0
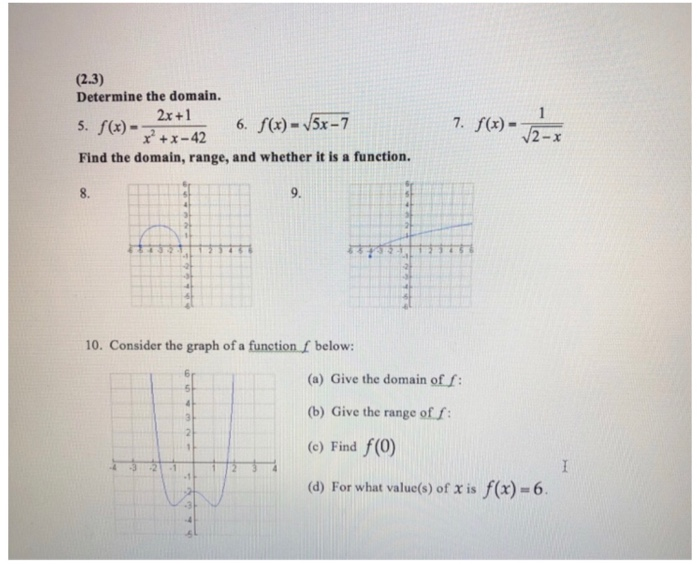



2 3 Determine The Domain 5 F X 6 F X 5x 7 Chegg Com




Ex 2 2 6 Determine Domain And Range Of R X X 5




Answered Find The Domain And Range Of The X Bartleby



Q Tbn And9gcqj529kunx E23asbmwgf8sdjnucswezuevva8edino5czgfbjv Usqp Cau
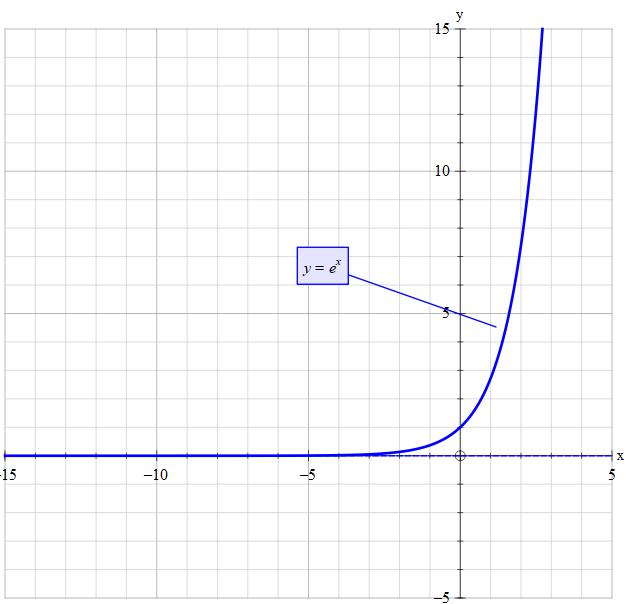



What Is The Domain And Range Of Y E X Socratic




Find The Domain And The Range Of The Function 4 F X 1 7x 5 For X 7 Homeworklib
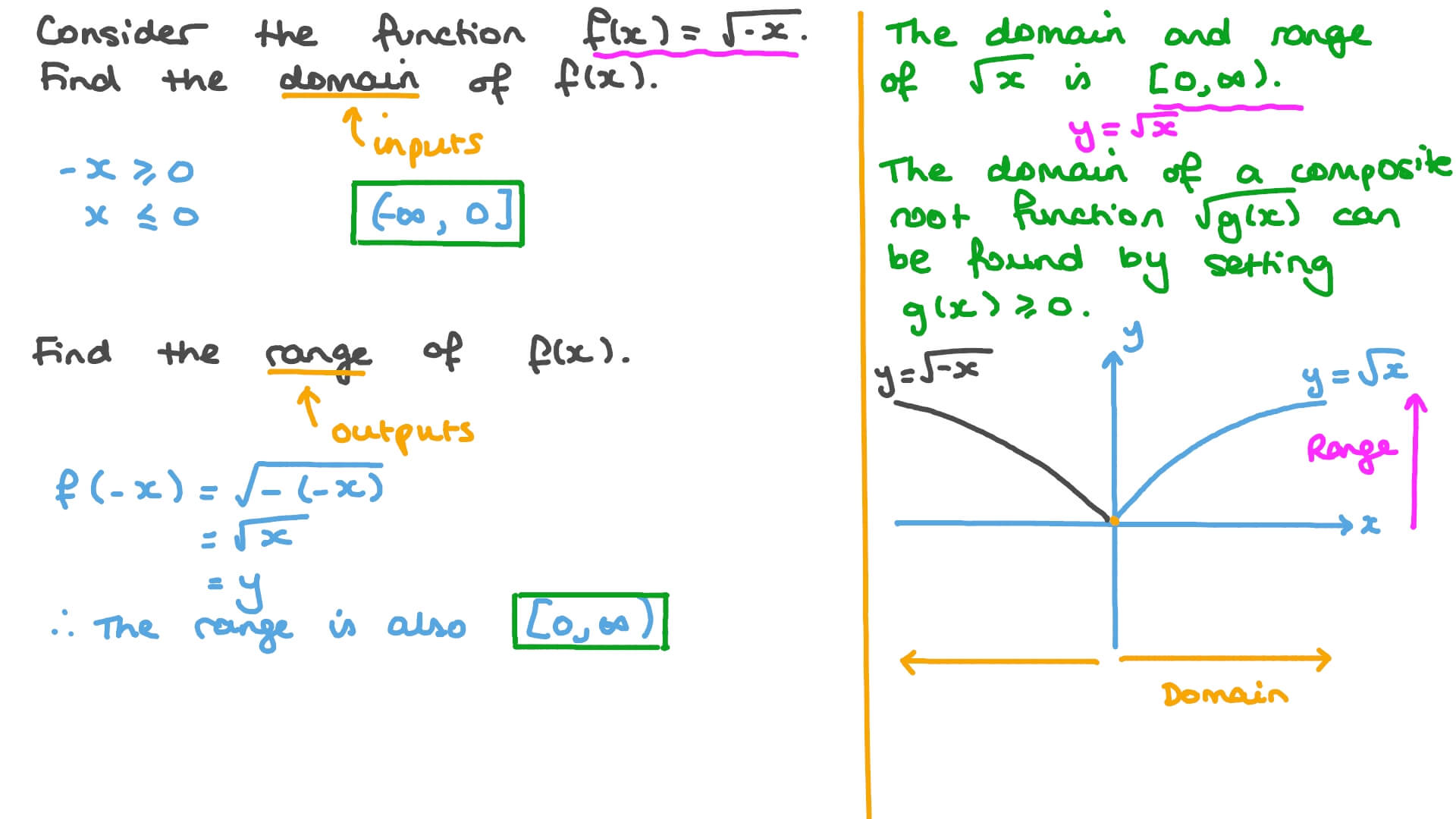



Question Video Finding The Domain And Range Of A Radical Function Nagwa




Find The Domain Of The Function F X X 2 3x 5 X 2 5x 4
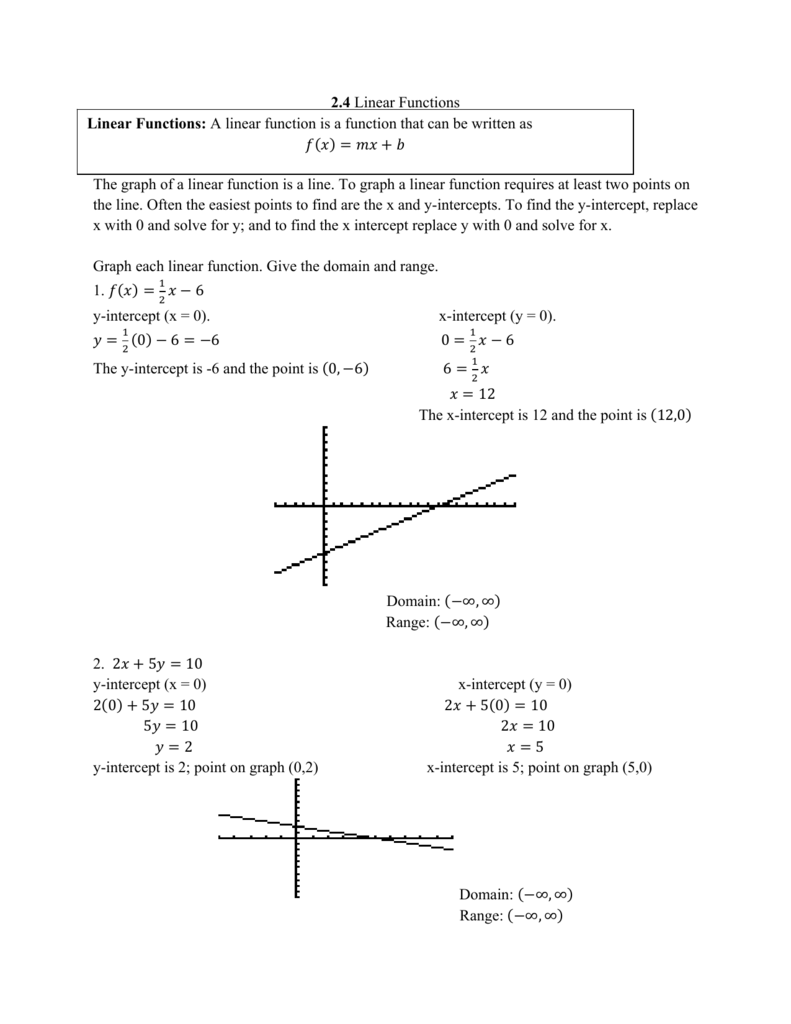



2 4 Linear Functions The Graph Of A Linear Function Is A Line To
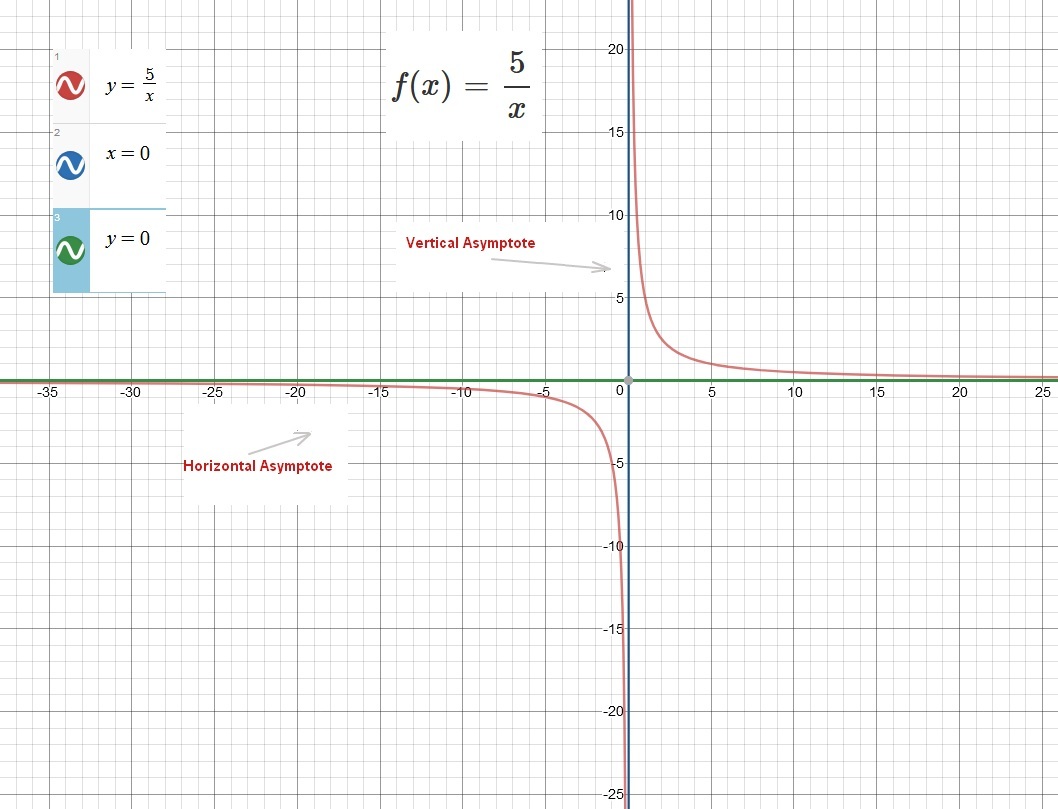



What Is The Domain And Range Of The Function F X 5 X Socratic



What Is The Domain And Range Of 1 X 3 Quora




Find The Inverse Function Of F State The Domain And Chegg Com



Find The Domain And Range Of F X 2x 5 Mathskey Com



3
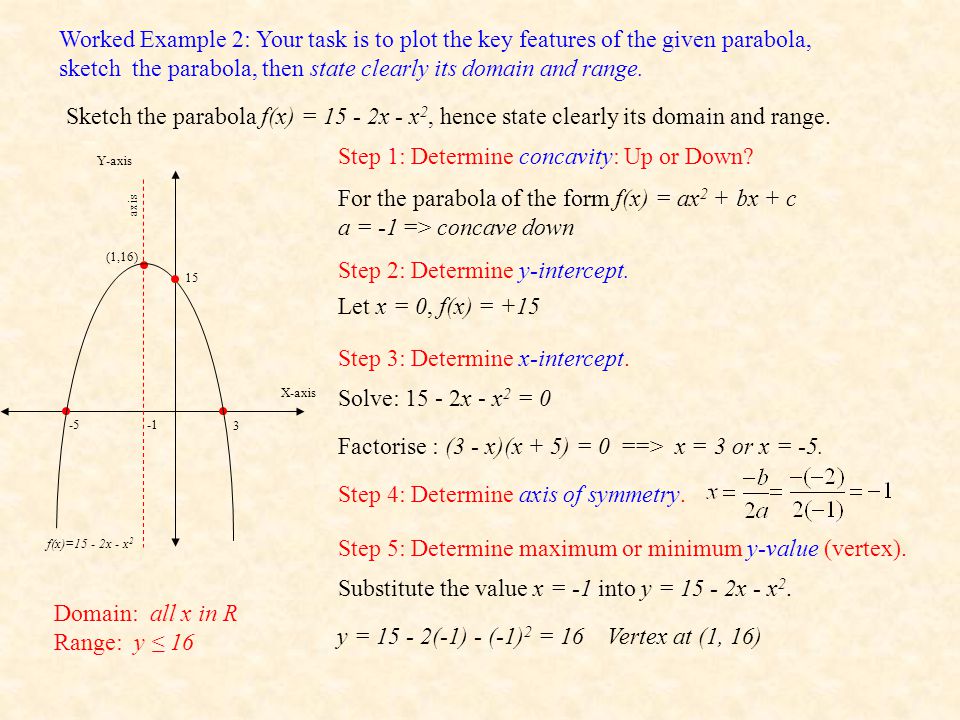



Functions Domain And Range By Mr Porter Ppt Download
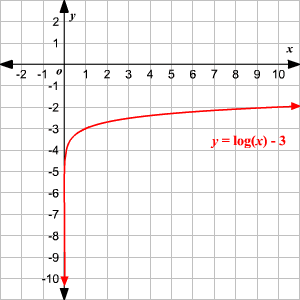



Domain And Range Of Exponential And Logarithmic Functions



For The Function F X X 2 5 Find The Domain And Range Enotes Com



Solution Find The Domain And Range Of The Function F X X 2 5x 6



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic
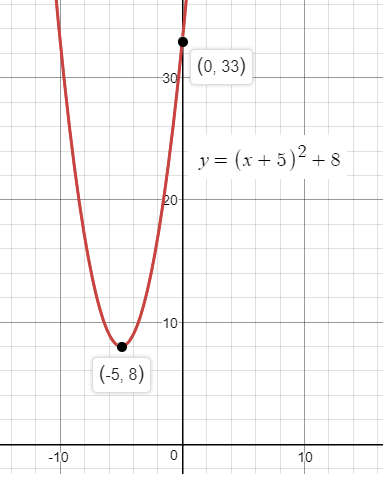



How Do You Find The Domain And Range Of F X X 5 2 8 Socratic




Domain And Range Calculator Wolfram Alpha




How To Find The Domain And Range Of A Function 14 Steps




What Are The Domain And Range Of The Exponential Function Below Tex F X 5 X 6 Tex Brainly Com




How To Find The Domain Of A Function Video Khan Academy
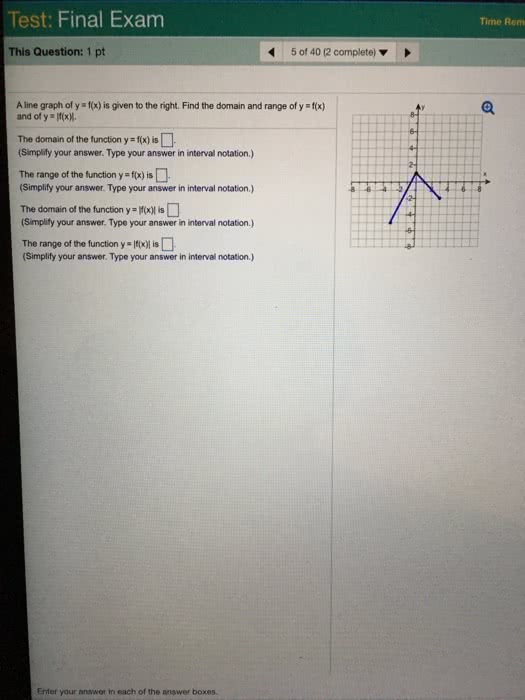



Oneclass A Line Graph Of Y F X Is Given To The Right Find The Domain And Range Of Y F X
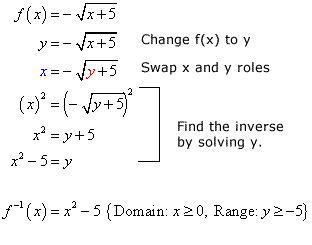



Inverse Of Square Root Function Chilimath




Introduction To Function Domain And Range Mohd Noor




Example 15 F X 1 X What Is The Domain And Range Examples
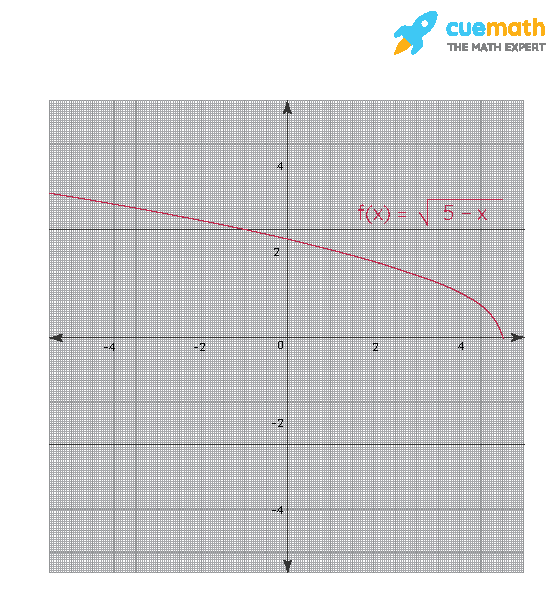



Give An Example Of A Function F X With A Domain Of 0 5 And A Range Of 0 Solved




Find The Domain And Range Of The Function F X 2 X 5
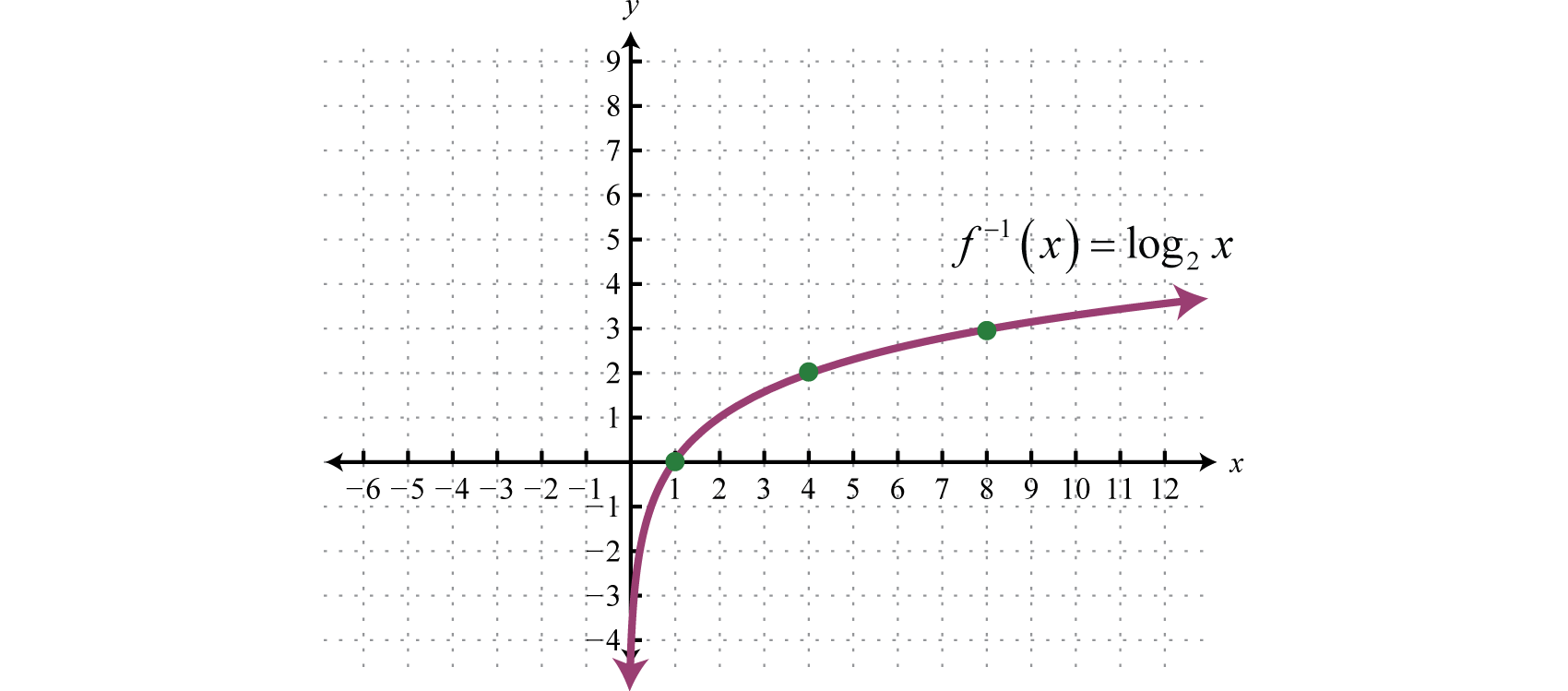



Logarithmic Functions And Their Graphs




The Domain Of The Function F X Sqrt 5 X X 2 6 Is A 3 2 Uu 2 3 B 3 2 Uu 2 3 C 3 2 Uu 2 3 D None Of These



1




Find The Domain And The Range Of The Real Function F X X 3 X 5 Youtube



How To Find Domain Of Function F X X 3x 5 X 5x 4 The Math Guru




Find Domain And Range Of Function Y 1 X Youtube




6 Ways To Find The Domain Of A Function Wikihow
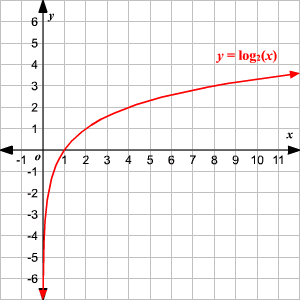



Domain And Range Of Exponential And Logarithmic Functions




Write Domain And Range Given An Equation College Algebra




Domain And Range Of Quadratic Functions Video Khan Academy




Answered The Function F Has A Domain Of 0 5 Bartleby




Find Domain Of X 2 5x 6 Mathematics Topperlearning Com Hv2l3nff
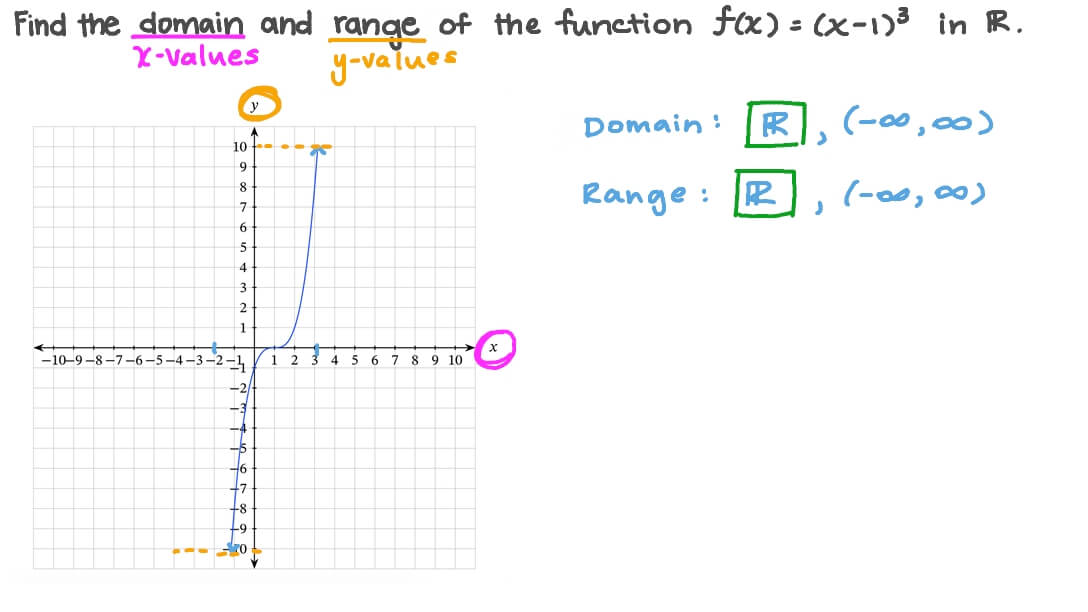



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa
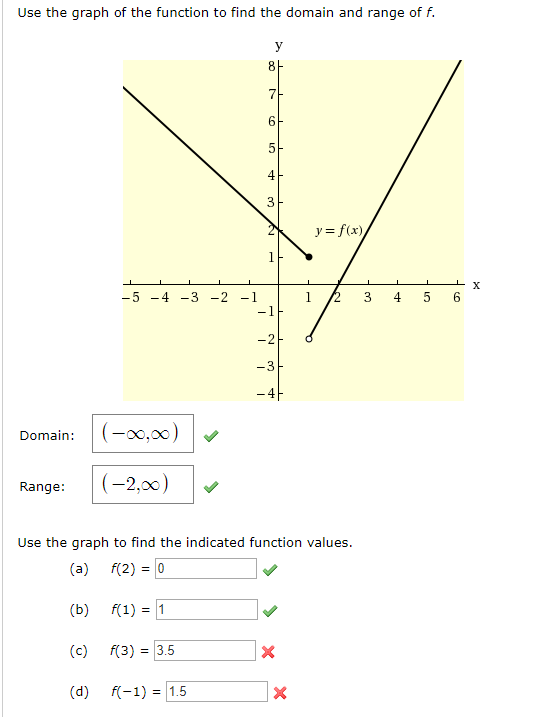



Use The Graph Of The Function To Find The Domain And Chegg Com



Q Tbn And9gcqpama6tqgin Iutakqatcksftftyjylbbujdpmxcrct Ee Usqp Cau




How To Find The Range Of A Function Video Khan Academy



Domain And Range Examples Domain And Range Of Functions




6 Ways To Find The Domain Of A Function Wikihow




What Are The Domain And Range Of The Function F X 3 X 5 2 4 Brainly Com




Use A Graph To Find The Range Of The Function Y F X X 2 16 On The Domain 4 Less Than Or Equal To X Less Than Or Equal To 5 Study Com




Tutorial Function Domain And Range Pdf Variable Mathematics Domain Of A Function




Domain Range And Codomain



Solved Activity 1 1 Answer The Guide Questions To Complete The Table Of Domain And Range Of The Following Exponential Functions A F X 5 Is F Course Hero




What Are The Domain And Range Of The Function F X 3 X 5 Brainly Com




Misc 5 Find Domain And Range Of F X X 1 Class 11




Domain Of Function F X X 1 5 X Donimain




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Find The Domain And The Range Of The Function F X X 2 25 X 5




How To Find The Domain And Range Of A Function 14 Steps



Domain And Range Algebra And Trigonometry




Find Domain And Range Of The Functions F X Sin 1 5x F X 1 X 2 X 3 1 X 2 F X Sinx X 2 5x 6 F X Log



Domain And Range



Www Olma Org Ourpages Auto 18 9 17 1 7 answers Pdf




Write Domain And Range Given An Equation College Algebra



Solution Range And Domain If F X 4x 2 4x 5 Find F 0
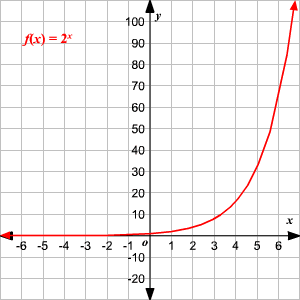



Domain And Range Of Exponential And Logarithmic Functions




What Are The Domain And Range Of F X 1 5 X En Ya Guru



What Is The Domain And Range Of 1 X 3 Quora
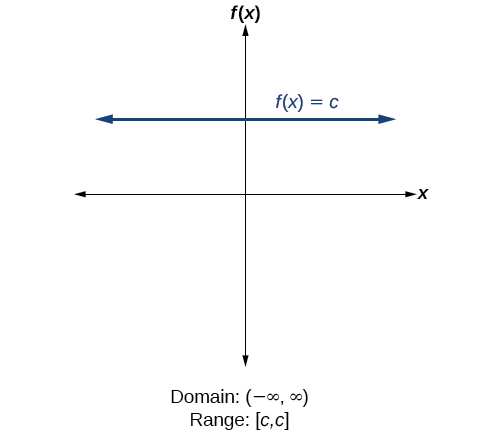



3 3 Domain And Range Mathematics Libretexts




Find The Domain And The Range Of The Function F X X 2 25 X 5 Youtube



0 件のコメント:
コメントを投稿